Imagine this, but with the shells infinitely thin (source).
The shell at distance $b$ from the center is also distance $a + dr$, since we're defining our shells to be $dr$ thick. We'll also say that the difference in energy density between a shell distance $a$ and distance $a+dr$ is $du$. Distributed throughout an entire shell of volume $4 \pi r^2 dr$, this means that shell $a$ has a total energy of $(u + du)(4 \pi r^2 dr)$, while shell $b$ has a total energy of $(u)(4 \pi r^2 dr)$. Note that the size of the shells here has stayed the same, as the difference between a shell distance $a$ from the center and distance $a+dr$ from the center is negligible enough that we can disregard it (which, again, the picture represents poorly). This means that the total excess energy between shell $a$ and shell $b$ is\[(u + du)(4 \pi r^2 dr) - (u)(4 \pi r^2 dr) = 4 \pi r^2 dr du\] Next we want to figure out $L(r)$, the equation for the net outward flow of energy (this can be thought of as the luminosity at different radii within a star). We have the excess in the total amount of energy, so to turn this into the outward flow of energy all we need to do is turn it into energy per time (luminosity) by dividing by the diffusion time. In this case, since we're looking at a distance of $dr$ rather than $R$, the diffusion time is $\frac{(dr)^2 \sigma_T \rho}{c \bar{m}}$. This results in the following for $L(r)$:\[L(r)=\frac{4 \pi r^2 c \bar{m}}{\sigma_T \rho}\frac{du}{dr}\]Finally, to turn this into $dT/dr$, we'll use our equation for the energy density of a blackbody, given by $u = aT^4$. Our first step will be to differentiate this, giving us \[\frac{du}{dr}=4aT(r)^3\frac{dT(r)}{dr}\] We can now plug this into the $du/dr$ term of $L(r)$ and solve for $dT(r)/dr$, which gets us to \[\frac{dT}{dr} = \frac{L(r)\sigma_T \rho}{16 \pi r^2 c \bar{m} aT(r)^3}\] Finally, knowing that $\kappa = \sigma/\rho$, we can substitute it in to get \[\frac{dT}{dr} = \frac{L(r) \kappa \rho}{16 \pi r^2 c a T(r)^3}\]This equation will be important soon, but so will a few others (which we've derived in the past) so we'll toss them up here as well. One is the equation for hydrostatic equilibrium, $dP/dr$, given in its most general form as\[dP/dr=\frac{GM^2}{4r^5}\]The other is the equation for mass conservation, $dM/dr$. This is a relatively straightforward derivation, starting with an integral of spherical shells integrated by mass. Each shell has volume $4\pi r^2 dr$ and volume $\rho r$, so we know that \[M(r) = \int_0^R 4\pi r^2 \rho (r) dr\]By the fundamental theorem of calculus, then, we know that $dM/dr = 4\pi r^2 \rho (r)$.
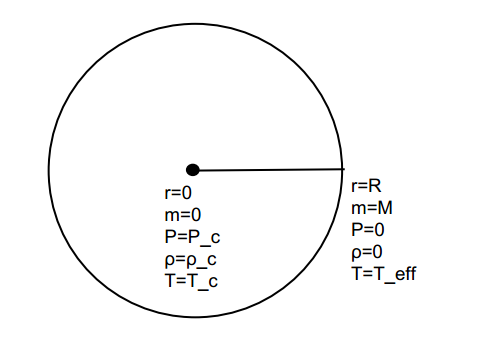
The last equation we're worried about is going to be the ideal gas law, relating the pressure and density of gas inside of a star. Chemistry students will know this as $PV=nRT$, but astronomers prefer $P=nk_bT$. However, since we're concerned with mass density rather than number density, we'll substitute $\rho/\bar{m}$ for $n$, giving us\[P=\frac{\rho}{\bar{m}}k_BT\]Now what we want to do is rewrite these equations as scaling relations, throwing away constants so we can really just strip things down to what changes with respect to what. We'll begin with $dP/dr$, first separating $dP$ and $dr$ to get \[dP = \frac{GM^2}{4R^5}dr\]4 and $G$ are constants, so we can ignore them. $dP$ scales with $P$, so we'll substitute $P$ for it, and $dr$ and $R$ scale together--so $dr/R^5$ actually goes as $1/R^4$. This gives us the final relationship\[P\sim \frac{M^2}{P^4}\]Next we'll think about $dT/dr$, which separates to give us $T^4dT = \frac{LM\kappa}{64\pi R^5ca}dr$. For this one the boundary conditions are especially important. The first of these is at the center of the sun, where $r = 0$, $m = 0$, and $\rho$, $P$, and $T$ are $\rho_C$, $P_C$, and $T_C$ (the core density, core pressure, and core temperature, respectively). The other is the edge of the Sun, where $r=R$, $m=M$, $\rho$ and $P$ are $0$, and $T=T_{eff}$, the effective temperature.
We need to be a bit more careful here about saying what $d-$ scales as what. $dT$ is, properly speaking, the change in temperature between $T_c$ and $T_{eff}$, or $T_c-T_{eff}$. However, since $T_c$ is in the neighborhood of a million Kelvin, and $T_{eff}$ is closer to six thousand, we can say that $dT$ goes as $T_c$ (and $T^3dT$ goes as $T_c^4$). Likewise, $dR$ is $R-R_0$, or $R-0$. Thus, the scaling relationship we end up with is\[T_c^4 \sim \frac{\kappa LM}{R^4}\]The last, and least exciting, scaling relationship comes from $dM = 4 \pi R^2 \rho(r) dr$. We know that $dM$ goes as $M$ and $dr$ goes as $R$, so when we plug in $M/R^3$ for $\rho(r)$, we get\[M\sim \frac{MR^3}{R^3}\sim M\]Not super enlightening, but it does make sense!
This is all we need to go on to start figuring out the scaling relationships we're really interested in. The $T_c$ versus $T_{eff}$ distinction is important when doing the initial derivation, but it turns out that the two scale equivalently, so we'll just use a generalized $T$ from here on out ($T_{eff}$ is ultimately going to matter more anyway). The first relation is mass-radius. We know that $P=\frac{\rho}{\bar{m}}k_BT \sim \frac{M}{R^3}T$, and that $P\sim \frac{M^2}{R^4}$. Substituting for $P$ then gives us $M\sim RT$ or, assuming a constant temperature, $M\sim R$. In other words, mass and radius scale linearly with one another. This will be extremely useful to know very soon.
We'll know look at the mass-luminosity scaling for very massive stars, where $\kappa$ can be assumed constant (meaning that the opacity of the star does not depend on temperature). Based on the scaling relationship we derived from $dT/dr$, this immediately tells us that $T^4\sim LM/R^4$. Now, using the fact that mass and radius scale linearly, we can substitute $M$ for $R$, then solve for $L$. This gives us \[L \sim T^4 M^3\] Or assuming constant $T$, $L\sim M^3$.
For low-mass stars, $\kappa$ gets a little more complicated, following what is known as the Kramer's Law opacity: $\kappa \sim \rho T^{-3.5}$. However, our methodology will be the same, starting with the statement that \[T\sim \frac{\rho T^{-3.5} LM}{R^4}\] Plugging in $M/R^3$ for $\rho$ and substituting $M$ for $R$, this simplifies to $T\sim M^2R^3T^{7.5}$. The reason we left three powers of $R$ in there is because we know, from our scaling relation $M\sim RT$, that $R\sim M/T$. Thus, we can plug this in for $R$ to get our powers of $T$ right (which is nice, though we'll end up considering them as constants anyway). This lets us boil things down to \[L\sim M^5T^{4.5}\sim M^5\]If we assume constant temperature.
Finally, we want to derive the relation between $T_{eff}$ and $L$--this is what lies at the heart of the H-R diagram. Since $L$ = $FR^2$ (luminosity equals flux times area), and that $F=\sigma T^4 \sim T^4$, we know that \[L\sim R^2T^4\sim M^2T^4\] For high-mass stars, we've figured out that $L\sim M^3$, so we'll plug in $L^{1/3}$ for $M$ in this case. This gives us $L\sim L^{2/3}T^4$. Getting all of the powers of $L$ on one side, we have the $L-T$ relationship for high-mass stars as \[L\sim T^{12}\]Pretty steep, huh? Let's see how it looks at the other end of the H-R diagram. For low-mass stars, we found that $L\sim M^5$, so we'll plug in $L^{1/5}$ for $M$. This gives us $L\sim L^{2/5}T^4$. Repeating the process we used for high-mass stars, we get an $L-T$ relation for low-mass stars as \[L\sim M^{20/3}\]Not quite as steep, but still pretty extreme. Since it's clear that the behavior of high- and low-mass stars is somewhat different, it's worth considering an intermediate model, which we'll represent as $L\sim M^4$. The $L-T$ relationship for these stars, derived in the same way, is $L\sim T^8$.
The H-R diagram, in case you forgot (source).
How can this be right when the H-R diagram looks so neatly linear, with the main sequence at such a pretty 45-degree angle? The answer is actually not all that exciting--it's just a question of scaling. Like most plots in astronomy, the H-R diagram is represented on a log-log scale, and while the horizontal axis only spans a few orders of magnitude, the vertical axis covers ten! Looking at the math behind the diagram is a helpful reminder that the best way to represent something visually isn't necessarily the least misleading!
Very nice!
ReplyDelete