a) The photon does not freely travel to the surface of the Sun. Instead it random walks, one collision at a time. Each step of the random walk traverses an average distance $l$, also known as the mean free path. On average, how many steps does the photon take to travel a distance $\Delta r$?
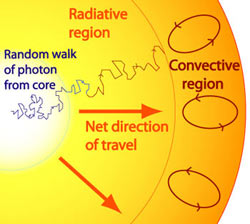
Key to understanding this question is recognizing that photons produced in the Sun do not follow a straight line straight from their source (in this case, nuclear fusion of Hydrogen atoms in the Sun's core) to Earth. Rather, they follow a random walk (alternatively known as a "drunkard's walk"), ricocheting from one proton, electron, or other photon into another in the dense interior of the Sun. Only when they reach the Sun's surface are they free to travel in a straight line.
The random walk of a photon to the Sun's surface (source).
The distance the photon travels during each step of this random walk we have defined as $l$. We'll next define $\vec{D}$ as a sum of vectors $\vec{r}_i$ with magnitude $l$. Since the direction of each vector $\vec{r}_i$ is random, however, then $\vec{D} = \sum \vec{r}_i$ is zero--if if every time you take a step, it's in a random direction, you're ultimately not going to end up very far from where you started. However, you will at times get very far away from your starting point before randomly making your way back, and this is key to understanding photons escaping the Sun. Since the Sun is not infinite, a photon must only make it as far as $R_\odot$ from its source. Once it is at the edge of the Sun, the random walk is over and it is free to propagate into space. Thus, we can remove the directional dependence of $\vec{D}$ by defining $\Delta r$ as $(\vec{D}^2)^{1/2}$.
Let's begin by solving for $\vec{D}^2$, remembering that it is originally defined as a sum of vectors, from 0 to $N$ (where $N$ is the number of steps it takes to go $\Delta r$ distance--in other words, what we're looking for). Note that, since these are vectors we're dealing with, the multiplication we're doing is actually a dot product. \[(\sum_{i=1}^N \vec{r}_i)^2 = \sum_{i=1}^N |\vec{r}_i||\vec{r}_i| cos(0) + \sum_{i,j}|\vec{r}_i||\vec{r}_j|cos(\theta)\] $\theta$ is the angle between vectors $\vec{r}_i$ and $\vec{r}_j$, which, since the directions of $\vec{r}_i$ and $\vec{r}_j$ are random, is an expectation value for an "average" direction. Mathematically, we can define it as \[\frac{1}{2\pi}\int_0^{2\pi} cos(\theta)d\theta = 0\] Thus, the second term in our squared summation is simply zero. As for the first term, since $|\vec{r}_i|$ is by definition $l$, we have \[\sum_{i=1}^N |\vec{r}_i||\vec{r}_i| cos(0) = \sum_{i=1}^N l^2 = Nl^2\] Remembering that this is equal to $\vec{D}^2$, we can next take the square root of $Nl^2$ and set it equal to $\Delta r$. Finally, we can solve for $N$, giving us \[N = (\frac{\Delta r}{l})^2\]
b) What is the photon's average velocity over this distance? Call this $v_{diff}$, the diffusion velocity.
Having wrapped our heads around the fact that a photon must actually travel $Nl$ distance in order to get $\Delta r$ away from its source, figuring out $v_{diff}$ is just a distance equals rate times time problem. We'll start by actually calculating $t_{diff}$, the diffusion time, since we know that the photons are actually moving at rate $c$--the speed of light--just not aways in the right direction. Thus, $Nl = c \times v_{diff}$, So $t_{diff} = \frac{Nl}{c}$. Plugging this all back into the distance-rate-time setup, we can now say that \[\Delta r = v_{diff} \times t_{diff} = \frac{v_{diff} Nl}{c}\] Solving for $v_{diff}$ gives us \[v_{diff} = \frac{\Delta r c}{Nl} = \frac{\Delta r c}{\frac{(\Delta r)^2}{l^2}l = \frac{cl}{\Delta r}\]
c) The `mean free path' $l$ is the characteristic (i.e. average) distance between collisions. Consider a photon moving through a cloud of electrons with a number density $n$. Each electron presents an effective cross-section $\sigma$ . How are these parameters related?
Electrons are pretty small, but they still do have a physical size. This is represented here by the quantity $\sigma$, which can be thought of as the "diameter" of a particle. Larger particles--such as protons and neutrons--have larger cross-sections, and are thus photons are more likely to hit them and scatter. Likewise, if particles are more dense, photons are similarly more likely to hit them and scatter.
Density and cross-section $\sigma$ of electrons in a volume of length $dx$ (source).
Establishing a relation between $l$, $n$, and $\sigma$ really is this simple. Since larger values of both $\sigma$ and $\n$ will yield smaller values of $l$--particles scattering more often will travel less far in between each instance of scattering--we can establish the relation $l = \frac{1}{\sigma n}$. A quick unit check shows that this works out dimensionally as well.
d) The mean free path length $l$ can also be related to the mass density of absorbers $\rho$ and the absorption coefficient $\kappa$ (cross-sectional area of absorbers per unit mass). How is $\kappa$ related to $\sigma$? Express $v_{diff}$ in terms of $\kappa$ and $\rho$ using dimensional analysis.
Once again, increasing both mass density and absorption will decrease $l$, so we can state that $l = \frac{1}{\kappa \rho}$ (and again, the units reassuringly check out). We can then just plug these in for $l$ in our equation for $v_{diff}$, which tells us that \[v_{diff} = \frac{c}{\kappa \rho \Delta r}\]
e) What is the diffusion timescale for a photon moving from the center of the sun to the surface? The cross section for electron scattering is $\sigma_T = 7 \times 10^{-25}$ cm$^2$ and you can assume pure atomic hydrogen for the Sun's interior.
We computed $t_{diff}$ way back in part b) as $\frac{Nl}{c} = \frac{\Delta r^2}{cl}$. We can now apply this here, using $R_\odot$ as $\Delta r$ and $\frac{1}{\sigma n}$ for $l$. The first step is to find $n$, which we can do by dividing the mass density of the Sun, $\rho_\odot = 1.5$ g cm$^{-3}$ by the mass of a hydrogen atom, $\bar{m} = 2 \times 10^{-24}$. All of this can then be plugged into our equation for $t_{diff}$. \[t_{diff} = \frac{R_\odot ^2 (\frac{\rho_\odot}{\bar{m}})\sigma_T}{c}=\frac{(7\times10^{10})^2\times1.5\times7\times10^{-25}}{2\times10^{-24}\times3\times10^{10}}\] This all comes out to about $10^{11}$ seconds--or more usefully expressed, 10,000 years. This means that, while it may take only eight minutes for a photon to travel one AU from the surface of the Sun to Earth, it took that photon billions of times as long just to travel less than .5% of the distance. Interestingly, it also means that if the Sun were to "go out" today, ceasing all production of energy in its core, we wouldn't find out until countless generations from now.

Great job Tom! A couple of typesetting issues you might want to look into.
ReplyDelete