This is a pretty general question, so it's important to start by examining what data we actually collect when we observe the radial velocity of a star and the light curve of a planetary transit. The first of these, the radial velocity curve, we have actually already discussed in great depth here, but we'll do a quick refresher course on that when we get around to using it. Right off the bat, though, we'll be working with the planet's lightcurve.
Lightcurve of WASP-10 b transit.
As you can see, there's a very obviously visible dip in the amount of light we're receiving from the host star, WASP-10, as the planet passes in front of it. As a matter of fact, we can derive a pretty substantial amount of information from the length, depth, and shape of this dip.
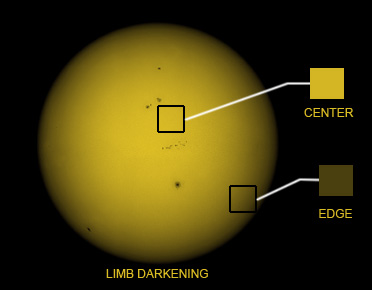
The sharply slanted edges are known as "ingress" and "egress," and are the time it takes for the planet to go from just barely overlapping with the outer edge of the star to sitting entirely in front of it. However, in between ingress and egress the brightness of the star isn't constant--it actually keeps getting dimmer until the very center of the transit. This is due to a process called "limb darkening," where the outer edge of a star's disc actually appears less bright than the center (it has to do with looking through more of the star's atmosphere, and is comparable to why stars are dimmer and harder to observe when they're close to the horizon). This phenomenon is easily visible on any high-resolution image of the Sun:
Example of limb darkening on the Sun (source).
We can also figure out the relative radii of the planet and star from the depth of the transit. Since the planet is emitting essentially no light, the flux received from the star should decrease by a factor equivalent to the area of the planet's disc ($\pi R_p ^2$) over the area of the star's disc ($\pi R_* ^2$), since the planet is blocking that fraction of the star's area, and thus light. If we define the depth of the transit as $\delta$, we can express this mathematically as\[\delta = \frac{R_p ^2 }{R_* ^2}\]On our lightcurve of WASP-10 b it looks like $\delta$ is around 0.3, so we know that the radius of the planet is around $\sqrt{0.03} \approx 1.7 \times 10^{-1}$ times the star's radius.
The next thing we can figure out from the lightcurve is the ratio of the star's radius to the planet's orbital semimajor axis.
The star on the left, with the planet shown at the start of its transit (top) and end of its transit (bottom). The orbital semimajor axis, a, and the radius of the star, $R_*$, are labeled.
As you can immediately see from the figure above, $tan(\theta) \approx \theta = R_*/a$. The ratio of the transit time to double this angle will be the same as the total period over the angle traversed over one period ($2\pi$, a full circle). Or, in equation form: \[\frac{t_t}{2\theta}=\frac{t_t}{\frac{R_*}{a}}=\frac{P}{2\pi}\]Rearranging this, we can see that the ratio of $a$ to $R_*$ is \[\frac{a}{R_*} = \frac{P}{2\pi t_t}\]If we had a longer lightcurve showing multiple transits we would be able to pull the period off of that, but we can also grab it off of the radial velocity curve (which will make an appearance in a few moments). As it happens, WASP-10 b has a 3.1-day period (meaning the planet's year lasts only 3.1 days!), and from the lightcurve we can tell that the transit time is right around 2 hours, so we can tell that the semimajor axis is 3.1 days/2 hours $\approx$ 12 times the radius of the star.
Now it gets both very messy and very cool. Density is defined as mass over volume, so we know that\[\rho_* = \frac{M_*}{4/3 \pi R_*^3}\]. We can also solve Kepler's third law for $a$ to give us \[a = \left(\frac{GM_*P^2}{4\pi^2}\right)^{1/3}\] The algebra from here gets sloppy and hard-to-follow, so we'll skip to the interesting part (if we were writing a textbook, this is where we would say that "the derivation is left as an exercise"). We can put these equations togetehr and solve for the density of the star in terms of known quantities, including the ratio of the semimajor axis to the star's radius:\[\rho_* = \left(\frac{a}{R_*}\right)^3\left(\frac{3\pi}{GP^2}\right)\]In the case of WASP-10, this gives us a density of 3.4 g cm$^{-3}$, or about 2.4 times the density of the Sun.
If we know the radius of the star, we can now figure out a few more definite quantities. Let's say $R_* \approx 0.8R_\odot$. From our semimajor axis-radius ratio, we can immediately say that WASP-10 b is orbiting at $12 \times 0.8 R_\odot = 6.7 \times 10^11$ cm. Since we also have an equation for the ratio of the planetary and stellar radius, we can also say that $R_p = 0.17 \times 0.8 R_\odot = 9.5 \times 10^9$ cm. Since we know the density of WASP-10, we can also compute its mass as $M_* = 3.4 \times 4/3 \pi (0.8 M_\odot)^3 = 2.5 \times 10^{33}$ g, or 1.2 $M_\odot$. The last value we can compute is the radial velocity of the planet, $K_p$. If we assume a circular orbit (and thus constant velocity), this means that $K_p$ can be related to $P$ and $a$ in a distance-rate-time equation, $K_p \times P = 2\pi a$. Solving for $K_p$ gives us a brisk $1.5 \times 10^7$ cm s$^{-1}$.
To continue, we'll finally break out that radial velocity chart.
As you can see, the star's radial velocity fluctuates from around -500 m/s to 500 m/s. This means that it's actually steadily moving around its orbit at this speed--we just only see it moving at that speed when it's going directly toward or away from us (remember, it's a radial velocity plot). Back when we were looking at these earlier, we found that $M_* v_* = M_p v_p$. Luckily for us, we've figured out three out of these four variables, and can now solve for the mass of the planet using the mass of the star and the radial velocities of each--it comes out to $M_p = 10^{31}$ g.
Lastly, but still important, we can figure out a quantity called the "impact parameter," which we'll denote as $b$. This is a value between 0 and 1 which quantifies how close the planet is to transiting directly across the star's equator ($b = 0$) and just skirting its edge ($b=1$).
Visualization of the impact parameter $b$. The planet moves along the horizontal line at the top (source).
$b$ is related to the depth of the transit $\delta$, along with the total transit time $T$ and the ingress time $\tau$ according to $b = 1 - \delta^{1/2}\frac{T}{\tau}$. We can estimate $\tau$ from the light curve to be about 0.3 hours, so finding $b$ is a simple matter of plugging and chugging--it comes out to be about 0.13.
So, summing everything up--from two plots and a given radius, we were able to find:
-The length of an exoplanet's year
-The density of its host star
-The mass of its host star
-The mass of the exoplanet itself
-The radius of the exoplanet
-The radial velocity of the exoplanet
-The radial velocity of the star
-The impact parameter of the planet.
We didn't do this, but we can also find the density of the exoplanet--it's an easy matter of dividing mass by volume. As it turns out, in this case $\rho_p = 2.8$ g s$^{-1}$.
Lots of thanks and credit goes to Anne Madoff, Scott Zhuge, Jennifer Shi, and Louise Decoppet for helping out with this one.




Great post! 4/4 + 1 bonus
ReplyDelete