Determining the Rotational Period of the Sun

BACKGROUND

Knowing the rotational period of the Sun $P_\odot$ is necessary in order to measure the physical size of the Sun, and in turn its distance from the Earth--for that reason alone, it is an interesting and worthwhile quantity to pin down. However, the rotational period of the sun is of interest in and of itself as well. The Sun plays host to massive amounts of charged plasma rising and falling within its interior. All of these particles are also rotating as the Sun turns--at varying rates depending on latitude, since the Sun is composed entirely of gas and plasma--making the system into a massive dynamo. The resulting electric field in turn is responsible for the Sun's magnetic field, which is responsible for the many effects clumped under the term solar activity--including sunspots (which will be very important momentarily), solar prominences and coronal mass ejections, and the aurorae (borealis and australis for the northern and southern lights, respectively). While our observations of the Sun's rotational period were undertaken as a component toward measuring the astronomical unit, knowing $P_\odot$ lays valuable groundwork for future investigation of the behavior of the Sun.

Left: The aurora borealis as seen (during the Perseid meteor shower!) in Colorado (Source)

Right: A 2012 solar prominence, which resulted in a CME (Source)

EQUIPMENT AND OBSERVATIONS

The key element of our observations was a system of mirrors functioning as a heliostat--a device which turns, compensating for the rotation of the Earth in order to constantly reflect light from the Sun at the same place. In our case, the heliostat reflected light from outdoors through an open window (leaving the window closed would diffract the light and complicate observations) onto another set of mirrors, which focused the reflected light from the Sun onto a piece of paper--and from there, our retinas. Setting up the heliostat required aligning sunlight through a pair of pinholes in order to ensure (without staring straight at it) that the Sun was shining on the primary mirror. The secondary mirror was then aimed at yet another mirror inside, which reflected onto a fourth mirror on a table, which in turn sent the light to a final mirror which reflected it down onto the paper on the surface of the table. Moving the last mirror closer to and farther from the penultimate one focused the image of the Sun--which, despite having been bounced all over the room, was still so bright that we needed to wear sunglasses when looking at it.

The heliostat. This image does not show the indoor mirrors that were used in tandem with those shown. (Source)

Throughout this process, the heliostat's motor was engaged, keeping the image stationary. After focusing the image of the Sun, we traced its outline onto the paper, and labeled all identifiable sunspots. Once this was done we turned off the heliostat motor, allowing the Sun to drift across the page as the Earth rotated. Tracing the line along which the sunspots drifted provided the terrestrial east-west line.

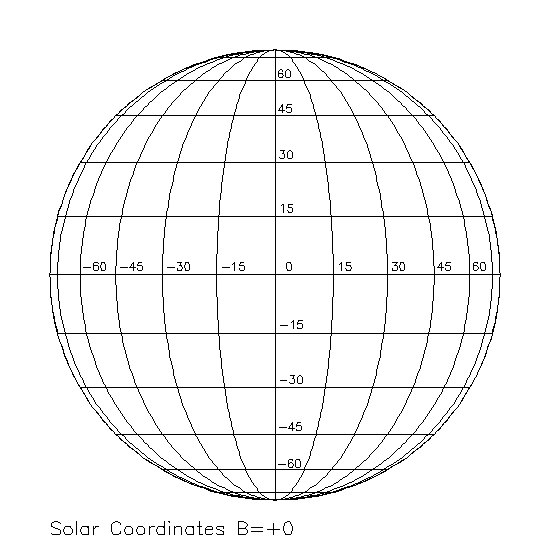
We repeated this process two more times, each a week apart. Once we had identified the same sunspots at various times, we could overlay the images (using the terrestrial east-west line to ensure that they were identically oriented) with a latitude-longitude grid identical to the one shown in order to see how the position of each sunspot on the disc of the Sun had changed since the last observation.

A solar latitude-longitude grid similar to the one we used. (Source)

RESULTS

Having tracked the position of a given sunspot from one week to the next, we could measure the angular change of its position on the face of the Sun itself. We could then set up the following relation between $\Delta t$--the change in time from one observation to the next--and $\Delta \theta$--the change in position. \[\frac{\Delta \theta}{360} = \frac{\Delta t}{P_\odot} \: \: (1)\] We collected data on five sunspots, which we labeled A, B, C, E, and F (another sunspot D was observed, but only at one point in time); the data for each is shown below.

Fig. 1: Observed $\Delta t$ and calculated $P_\odot$

Altogether, the (admittedly, widely variable) quantities measured for $P_\odot$ yielded an average value of 28.3 days. However, what we are measuring here is not exactly the rotational period of the Sun--at least, not the one we're looking for. It is possible to define two separate rotational periods for the Sun: the sidereal and synodic rotational periods. The sidereal period is the time it takes for the Sun to rotate once on its axis, and it's what we want, at least for the purposes of calculating the physical size of the Sun down the line. The synodic period is the time it takes for a point on the Sun to make a full revolution with respect to the Earth. Since the Earth is orbiting around the Sun in the same direction as its rotation, this requires a spot on the Sun to make a full rotation, and then continue rotating to catch up with the progress Earth has made in its orbit. The relation between sidereal (which we will continue to refer to as $P_{\odot}$) and synodic ($P_{sy, \odot}$) periods can be roughly expressed as follows:\[P_{sy, \odot} = P_{\odot}(1+\frac{R_{sy, \odot}}{365}) \: \: (2)\] If we plug in our average value for $P_{sy, \odot}$ of 28.3 days and solve for $P_{\odot}$, giving us a sidereal period of 26.3 days.

CONCLUSIONS

Clearly, our observations included a great deal of error, as our seven calculated values of $P_\odot$ varied from 14 to 48 days--giving us a hefty standard deviation of 13.2 days. This was likely the result of human error and our imprecise methodology, as the grid-overlay method of measuring $\Delta \theta$ by eye was extremely approximate. While it is difficult to accurately project and measure angular change over a sphere on a flat surface, if we were to repeat the process with the goal of improving accuracy, a more precise method would be needed. Additional measurements would also help to narrow down the value to a more accurate average.

However, this is actually a much more complicated problem than it initially presents as. As was previously mentioned, the Sun rotates at different rates over varying solar latitudes, and the variation in rotation rate rate for sunspots of higher or lower latitude. This motion is dependent on the Sun's rotation, but goes unaccounted for in our measurements.

However, our average $P_\odot$ of 26.3 days is a very good estimate of the literature value for the Sun's equatorial rotation period, 24.47 days. Thus, while the error inherent in our measurements was substantial, the seven trials we performed yielded an average which, while in need of significant refinement, serves as a fair estimate of the Sun's sidereal rotation period.