The Story of AY Sixteenus: Part I

Sketch the elevation of the star AY Sixteenus that is located at RA = 18 hours and Dec = +32 degrees along the meridian as a function of time (month) throughout the year as viewed from Mt. Hopkins, Arizona. Your sketch should be qualitative, yet clear, as if you were showing it to a class you are teaching. But don't be one of those teachers with horrible handwriting/drawing skills: neatness counts. Label each monthly point with the UT (Universal Time) that the star is on the meridian. What is the corresponding LST at each point?

Right Ascension (RA) and Declination (Dec) are the celestial sphere's analog of longitude and latitude, respectively. Declination is by far the simpler of the two--it's just latitudes on Earth projected out onto the sky. A star that orbits directly above the equator has zero declination, a star whose orbit takes it directly above us in Cambridge (42 degrees longitude) has a declination of 42 degrees, a star that sits directly above the North Pole (90 degrees latitude) has a declination of 90 degrees... You get the point. 

RA (which is measured in hours and minutes) is a bit more complex, since (just like longitude) it has to be measured from an arbitrary position. In the same way that people chose the Royal Observatory in Greenwich as zero degrees longitude, astronomers have picked the "first point of Aries," or the place in the sky where the sun sits at the Vernal equinox, as zero degrees RA. You can also think of this as being the one of the intersections of the ecliptic (the plane in which most of the planets orbit) and the celestial equator, which you can imagine these both as great circles arcing over your head. 

A section of the sky, showing the intersection of the ecliptic and horizon (Source)

RA is measured as the distance around the equator in a circle starting at Aries. Since every star has a permanent RA coordinate, the range of RA you can see is constantly changing as the Earth rotates. However, since the Earth is also circling the sun along its orbit, each day's rotation doesn't translate to 24 hours of RA--at this time tomorrow, I'll be looking at a slightly different patch of sky than I am right now (about four minutes of longitudinal difference). This also means that, while the right ascension of stars doesn't change, the sun's does, making a full circle every year. On March 21st at the vernal equinox the sun's RA is 00:00, three months later at the northern hemisphere's summer solstice it's 06:00, at the autumnal equinox it's 12:00, at the winter solstice it's 18:00, and by the time March 21st rolls around again it's back to 00:00 and we've made a full orbit. 

Local Sidereal Time (LST) is a related concept, and thankfully it's a simpler one. It essentially refers to whatever RA is crossing your meridian at a given time. So if it's March 21st and the sun is on my meridian, my LST is 00:00. Likewise, if a star should happen to have an RA of 18:00 (remember, the RA of stars other than the sun doesn't change), my LST will be 18:00 when it crosses my meridian. As I mentioned above, the sun's RA is 18:00 on the Winter Solstice, so on that day our LST will be 18:00 at noon. Time is determined by the sun, so a month (or two hours or RA) later, our LST will be 18:00 two hours before noon--extrapolating throughout the year, we can tell that LST = 18:00 will occur at 06:00 on the vernal equinox, midnight on the summer solstice, 18:00 on the autumnal equinox, and will be back at noon come late December.

All right, so let's come back to AY Sixteenus. What we know is this:

-Its declination, 32 degrees North (or +32 degrees, for those of you who find +/- more intuitive than N/S)

-Its RA, 18:00 hours

-Our own latitude, 32 degrees North

And that's all we need! If you've been paying attention, you should have already realized that the question is actually a very straightforward one--and that you're in store for the two least interesting graphs of all time. I'm feeling artistic today, so here's a diagram of what the setup looks like when the star is crossing our meridian.

Since stars' declinations don't change, that means that they trace the exact same path in the sky every day--you just sometimes can't see them because the sun occasionally happens to be in the way. Since AY Sixteenus has the same declination as our latitude, it's going to be directly overhead whenever it does this, regardless of what time of year it is. So here's boring graph #1:

Not Pictured: A Dependent Variable

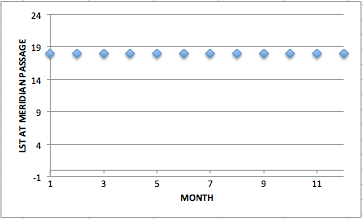
Figuring our LST at the star's meridian passage is going to end similarly. Since LST is defined as the RA of all the objects on your meridian, and AY Sixteenus' RA is 18:00, well...

We can figure out what time it will be for each of these meridian passages by using the calculations we did for the time of LST = 18:00 earlier. Knowing that it'll occur at noon in late December and move two hours earlier every month, it's easy to put it together into a neat little table.